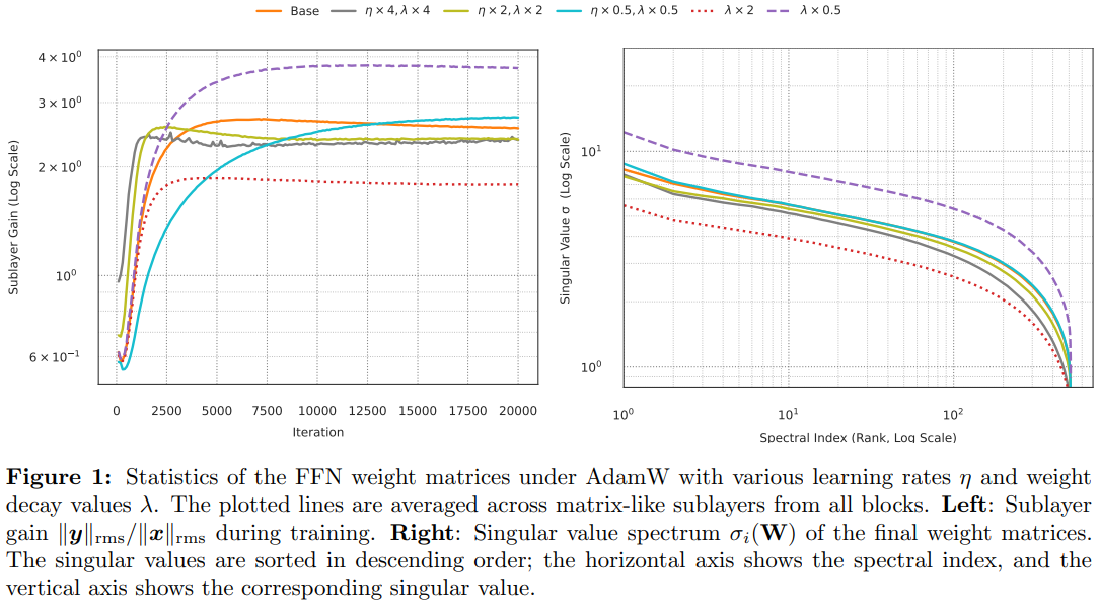
经验缩放定律规定了如何分配参数、数据和计算，而最大更新参数化（μP）通过均衡早期更新幅度实现跨宽度的学习率迁移。 然而，在现代尺度不变架构中，训练很快进入由优化器控制的稳定状态，其中归一化层会产生向后的尺度敏感性，有效学习率变得依赖于宽度，从而降低 μP 迁移率。 我们通过为 AdamW 引入权重衰减缩放规则来解决这个问题，该规则可以保持跨宽度的子层增益。根据经验，每个矩阵参数的奇异值谱在范数中按 \(\sqrt{\eta/\lambda}\) 缩放，形状近似不变；在宽度缩放 \(d\) 下，我们观察到顶部奇异值按\(\sqrt{\eta/\lambda}\cdot d^{0.75}\)缩放。 将此观察结果与矩阵类参数的 μP 学习率规则 \(\eta_2 \propto d^{-1}\) 相结合，意味着经验权重衰减缩放规则 \(\lambda_2 \propto \sqrt{d}\) ，该规则近似保持子层增益宽度不变。结合在 \(\eta_1=\Theta_d(1)\) 和 \(\lambda_1=0\) 处训练的类向量参数，这实现了学习率和权重衰减从代理宽度到目标宽度的零样本迁移，消除了每个宽度的扫描。 我们在 LLaMA 风格的 Transformer 上以及最小合成设置中验证了该规则，并提供了一种简单的诊断方法，即匹配顶部奇异值，以检查子层增益不变性。我们的结果通过明确控制优化器设置的稳态尺度，将 μP 扩展到接近初始状态之外，为 AdamW 下的宽度稳健超参数迁移提供了一种实用方法。

Empirical scaling laws prescribe how to allocate parameters, data, and compute, while maximal-update parameterization (μP) enables learning-rate transfer across widths by equalizing early-time update magnitudes. However, in modern scale-invariant architectures, training quickly enters an optimizer-governed steady state where normalization layers create backward scale sensitivity and the effective learning rate becomes width dependent, degrading μP transfer. We address this by introducing a weight-decay scaling rule for AdamW that preserves sublayer gain across widths. Empirically, the singular-value spectrum of each matrix parameter scales in norm as \(\sqrt{\eta/\lambda}\) with an approximately invariant shape; under width scaling \(d\), we observe that the top singular value scales approximately as \(\sqrt{\eta/\lambda}\cdot d^{0.75}\). Combining this observation with the μP learning-rate rule \(\eta_2 \propto d^{-1}\) for matrix-like parameters implies an empirical weight-decay scaling rule \(\lambda_2 \propto \sqrt{d}\) that approximately keeps sublayer gains width invariant. Together with vector-like parameters trained at \(\eta_1=\Theta_d(1)\) and \(\lambda_1=0\), this yields zero-shot transfer of both learning rate and weight decay from proxy to target widths, removing per-width sweeps. We validate the rule on LLaMA-style Transformers and in a minimal synthetic setting, and we provide a simple diagnostic, matching top singular values, to check sublayer-gain invariance. Our results extend μP beyond the near-init regime by explicitly controlling steady-state scales set by the optimizer, offering a practical recipe for width-robust hyperparameter transfer under AdamW.