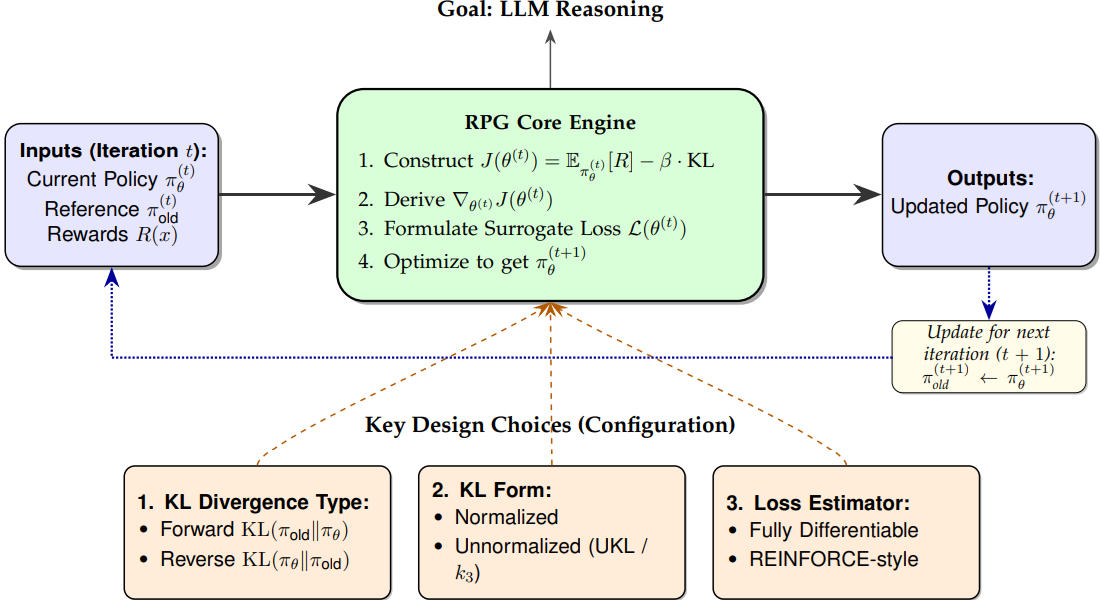
策略梯度算法已成功应用于增强大型语言模型（LLM）的推理能力。尽管Kullback-Leibler（KL）正则化在策略梯度算法中被广泛用于稳定训练，但对如何估计不同的KL散度公式并将其整合到在线强化学习（RL）的替代损失函数中的系统探索提供了一个微妙而系统可探索的设计空间。 在本文中，我们提出了正则化策略梯度（RPG），这是一个在在线RL设置中推导和分析KL正则化策略斜率方法的系统框架。我们推导了由正向和反向KL散度正则化的目标的策略梯度和相应的替代损失函数，同时考虑了归一化和非归一化的策略分布。此外，我们提出了完全可微损失函数的推导以及REINFORCE风格的梯度估计器，以适应不同的算法需求。 我们使用这些方法对LLM推理的RL进行了广泛的实验，与GRPO、REINFORCE++和DAPO等强基线相比，在训练稳定性和性能方面取得了改进或具有竞争力的结果。

Policy gradient algorithms have been successfully applied to enhance the reasoning capabilities of large language models (LLMs). Despite the widespread use of Kullback-Leibler (KL) regularization in policy gradient algorithms to stabilize training, the systematic exploration of how different KL divergence formulations can be estimated and integrated into surrogate loss functions for online reinforcement learning (RL) presents a nuanced and systematically explorable design space. In this paper, we propose regularized policy gradient (RPG), a systematic framework for deriving and analyzing KL-regularized policy gradient methods in the online RL setting. We derive policy gradients and corresponding surrogate loss functions for objectives regularized by both forward and reverse KL divergences, considering both normalized and unnormalized policy distributions. Furthermore, we present derivations for fully differentiable loss functions as well as REINFORCE-style gradient estimators, accommodating diverse algorithmic needs. We conduct extensive experiments on RL for LLM reasoning using these methods, showing improved or competitive results in terms of training stability and performance compared to strong baselines such as GRPO, REINFORCE++, and DAPO.